In case you haven’t heard by now heads up limit hold’em has been solved. You can read the original scientific paper here
https://webdocs.cs.ualberta.ca/~bowling/papers/15science.pdf
You can query the GTO bot named Cepheus’ strategy here http://poker.srv.ualberta.ca/strategy
But it’s slow and not really displayed in an easy to understand way for humans emulate. It’s not easy to figure out if it tends to check back certain boards or what its cbet % is for example. I was curious if you could download the code and run it yourself and how much it would cost. The good news is you can download and run it yourself, the bad news it’s going to cost you a lot to get an exact Cepheus replica($500k by my estimate).
Cost of computing estimate
Looking at http://aws.amazon.com/ec2/pricing/
A large compute optimized on-demand instance with 32 2.6-GHz Intel Xeon cores, 60 GB of RAM, and 320-GB of local disk is probably the most similar node to the ones used by the Alberta researchers. They cost $1.68 per hour. To run 200 of them for 68.5 days would cost you 200*1.68*24*68.5=$552,384
Of course computing cost decreases over time over time as shown by the graph below. In a five years this computation cost should be one tenth of this current estimate and we’ll have 10TB hardrives for $50(current cost of 1TB hardrives http://www.amazon.com/Seagate-Desktop-3-5-Inch-Internal-ST1000DM003/dp/B005T3GRNW) and be able to download and save the whole strategy easily on our home computer.

Source: http://hblok.net/storage_data/storage_memory_prices-2013-02.png
Scientific Paper Interesting Stats
There were a few interesting stats given in the paper that I don’t feel were talked about much by the media because it wasn’t explained all that well and put in normal “poker speak” terms. They referred to a “hand” as a “game” and measured edges in “milli-big-blinds/game” instead of a more typical “bb/100”.
The maximum achievable winrate playing vs Cepheus is listed in the paper as 0.986 milli-big-blind per game(by game they mean hand). In poker terms this equates to (0.986 milli big blinds / hand) * (1 big blind / 1000 milli big blinds) * (100) = 0.986 * .1 = 0.0986 bb/100 maximum winrate. So for example if you were playing true GTO headsup $200/$400 limit holdem vs Cepheus you could expect to win about $200 * 0.0986 = $19.72 per hour per table.
Some major troll nits were complaining that if it’s possible to have a positive winrate vs Cepheus then heads up limit hold’em isn’t solved. What I would say to these people is
a) 0.1 bb/100 achievable winrate is tiny and
b) if they really want to get this number lower they can do so by simply turning their algorithm back on and letting it run more iterations.
It lists the button’s winrate vs itself as “between 87.7 and 89.7 mbb/g for the dealer” This means the GTO edge for the button vs the big blind is 88 * 0.1 = 8.8 bb/100. So in other words when someone hit and runs one hand with their button vs you they’re stealing 0.088bb or $17.6 at $200/$400 in EV from you.
Reducing computation cost
There are a number of ways you could create a much cheaper “good enough” GTO bot yourself. The way that they created Cepheus is by running this code http://webdocs.cs.ualberta.ca/~games/poker/software/CFR_plus.tar.bz2 on a 200 node cluster of computers for 68 days. It is described in the paper as
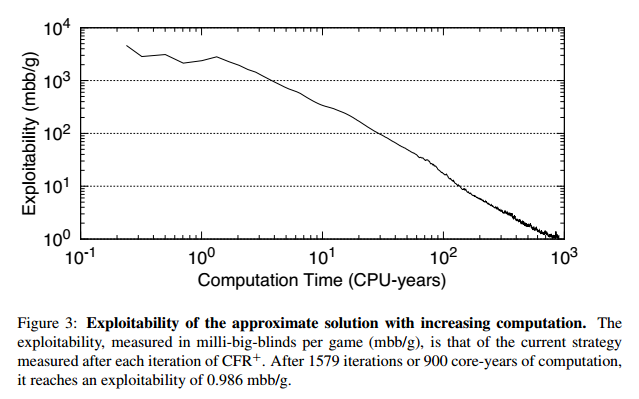
Our CFR+ implementation was executed on a cluster of 200 computation nodes each with 24 2.1-GHz AMD cores, 32GB of RAM, and a 1-TB local disk. We divided the game into 110,565 subgames (partitioned according to preflop betting, flop cards, and flop betting). The subgames were split among 199 worker nodes, with one parent node responsible for the initial portion of the game tree. The worker nodes performed their updates in parallel, passing values back to the parent node for it to perform its update, taking 61 minutes on average to complete one iteration. The computation was then run for 1579 iterations, taking 68.5 days, and using a total of 900 core-years of computation (43) and 10.9 TB of disk space, including filesystem overhead from the large number of files.
If you simply reduced the number of iterations ran you could create a not quite as good bot for a fraction of the cost. See the figure below from the scientific paper. Since they ran their sim for 900 core years or 1579 iterations they achieved a maximum exploitability of ~0.1 bb/100 (~$500k computation cost). Interpolating this graph that means that in 90 core-years of computation you could create a a bot with 1 bb/100 of exploitablity (~$50k computation cost). After 27 core-years computation cost you could create a bot with 10 bb/100 of exploitability (~$17k computation cost). After 9 core-years computation cost you could create a bot with 30 bb/100 of exploitability (~$5k computation cost).
You could further reduce computation cost by reducing the number of subgames. They solved for 110,565 subgames and their preflop strategy is very easy to view and download here http://poker.srv.ualberta.ca/preflop. You could hard code this in and reduce your computation cost drastically. Unfortunately at this time I haven’t worked out the math on how they arrive at 110,565 to calculate exactly what order of magnitude of computation this may save. If someone could help me out with that it would be greatly appreciated. There’s only 169 different preflop hand combinations, 1755 different flops each with 47 different turn cards and 46 different river cards.
Other games and online poker’s future
Their algorithm could easily be adapted to other limit games. Headsup limit Omaha 8 or better should be considered solved as well at this point. If someone wants to give me $1 million I’ll prove it. Same goes for headsup 2-7 triple draw. The stud games have a much higher number of game states so they may not be cheaply solvable at this point. Razz on the other hand ignores suits and only has 13 unique cards so a “good enough” headsup GTO bot (one with say 1bb/100 exploitability) could probably be created for $50k or less in computation cost at this point. It’s all a matter of time before all the games are dead and solved.
Some people will point out that the game state size of a no limit game is huge and may never be solved in our lifetime.
http://poker.cs.ualberta.ca/publications/2013-techreport-nl-size.pdf
Sure, it’s true that we may not see a Headsup No Limit Hold’em bot with maximum exploitability of less than 0.1bb/100 in our lifetime. That does not mean a “good enough” no limit bot with artificial pot size bet constraints (can only bet pot, 1/2 pot, 1/4 pot for instance) with less than 1 bb/100 of maximum exploitability could not be created TODAY for a couple hundred thousand.
It’s just a race to see who can figure it out first. The nosebleed guys hire programmers to figure out things out for them. They have the most money, resources and incentive to do so. It’s no secret at this point. I’m not optimistic about online poker’s future. Nobody plays online chess for money. Then again they do play online blackjack.
A more plain english summary of the paper is available here
http://spectrum.ieee.org/tech-talk/computing/software/computers-conquer-texas-holdem-poker-for-first-time
You can play against Cepheus here
http://poker-play.srv.ualberta.ca/