One of the benefits of writing these Elo explanations up is my readers can hopefully find any errors. My boy @ericrodawig was asking if the 1550 vs 1450 matchup should result in 1550 having a higher rating afterwards. My reply was no because the way Elo ratings are supposed to work is a rating only improves if their actual winrate exceeds their expected winrate. As 538 explains it
Autocorrelation is the tendency of a time series to be correlated with its past and future values. Let me put this into football terms. Imagine I have the Dallas Cowboys rated at 1550 before a game against the Philadelphia Eagles. Their rating will go up if they win and go down if they lose. But it should be 1550 after the game, on average. That’s important, because it means that I’ve accounted for all the information you’ve given me efficiently. If I expected the Cowboys’ rating to rise to 1575 on average after the game, I should have rated them more highly to begin with.
It’s true that if I have the Cowboys favored against the Eagles, they should win more often than they lose. But the way I was originally designed, I can compensate by subtracting more points for a loss than I give them for a win. Everything balances out rather elegantly.
However it did get me curious so I ran some sims and did find a slight autocorrelation. If you run 1550 vs 1450 matchup 1000 times, you should expect the 1550 to win ~640 times and 1450 to win ~360 times and their ratings should end up right back where they started. However, I found that 1550 tends to end up slightly higher, a bit below 1552 on average. I’m not 100% sure why this is, but in an ideal world this doesn’t happen and the autocorrelation is bad – unless you believe in the streak theory that wins are more likely after wins and losses are more likely after losses. My theory is that it is due to a non perfect win probability function. I’ve tried a different win probability function which I found posted somewhere
def alt_win_probability(p1, p2):
diff = p1 - p2
p = 1 - 1 / (1 + math.exp(0.00583 * diff - 0.0505))
return p
which is highly correlated to the original
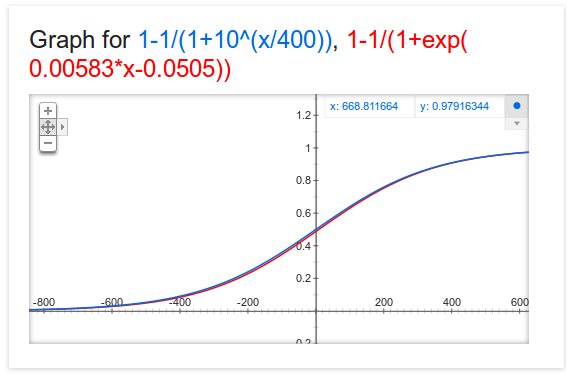
and this one tends to leave the 1550 slightly lower on average overall. A perfect win probability for this matchup is actually around 0.637, but we’re splicing hairs at this point. No model is going to be perfect and as the famous quote goes “All models are wrong, but some useful.”